The Station-to-Station (STS) protocol – Public-Key Cryptography

7.9.1 The Station-to-Station (STS) protocol

A simple example that nicely illustrates fundamental design principles of an authenticated key agreement protocol is the Station-to-Station (STS) protocol [136]. The protocol is a combination of Diffie-Hellman key agreement and the exchange of digital signatures for authentication, a concept we will explain in a minute.

Figure 7.5 shows the basic STS protocol. Recall that eK(i) denotes the encryption of input i under the shared secret key K using a symmetric encryption algorithm e. A hash function is a function that maps an input of arbitrary length onto an input of fixed length, denoted here by h(i) where i is the input. The input can consist of multiple parts i0,i1,…ij that are concatenated to a single bit vector i0|i1|…|ij. Note that in order to be useful in cryptography, hash functions need to fulfill some additional properties, which we will discuss at length in Chapter 11, Hash Functions and Message Authentication Codes.

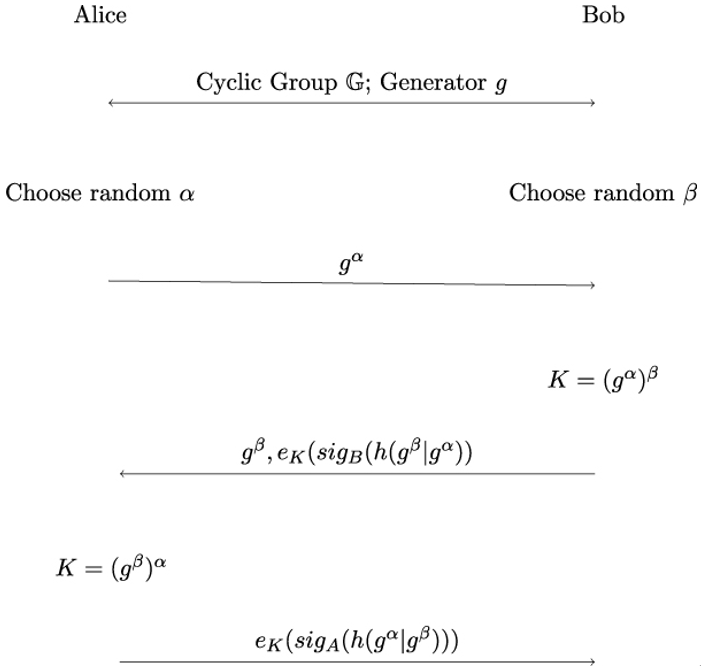
Figure 7.5: Basic STS protocol

Finally, sigA(i) denotes a digital signature for input i generated with Alice’s private key and sigB(i) denotes a digital signature generated with Bob’s private key.

Digital signatures are a new concept we will have much more to say about in Chapter 9, Digital Signatures. For now, it is sufficient to know that a digital signature is generated using the communicating party’s private key, which is, by design, only known to that party, and can be verified using that party’s public key, which is known to all communicating parties.

As a result, only Alice can compute sigA(i) and only Bob can compute sigB(i). But they both can verify each other’s signatures (for the input i, given that the input is known to the verifying party).

Note how the authenticity of Alice’s and Bob’s public keys plays a crucial role in the protocol’s security: if Mallory can trick Alice into believing that a public key PKM generated by Mallory belongs to Bob, she can easily impersonate Bob by presenting Alice with a fake digital signature sigM(i) instead of the genuine sigB(i).

The basic STS protocol in Figure 7.5 starts with Alice choosing a random number α and transmitting the exponential gα to Bob. Bob, in turn, chooses a random β and computes K = (gα)β. He then sends Alice the exponential gβ and signature of concatenated exponentials gβ|gα encrypted with a symmetric key encryption algorithm under key K.

Upon receiving Bob’s message, Alice computes K = (gβ)α. She then decrypts Bob’s encrypted signature eK(sigB(h(gβ|gα))) using key K she just computed and verifies the signature sigB(h(gβ|gα)) using Bob’s public key.