
7.7 The RSA algorithm
The RSA algorithm is named after its inventors, Ron Rivest, Adi Shamir, and Len Adleman (see Chapter 1, The Role of Cryptography in a Connected World, for a photo). Its trapdoor mechanism is based on the assumption that factoring, that is, finding the prime factors of a large integer n, is hard, while the inverse problem, namely multiplying prime factors to get n, is easy. While this trapdoor is certainly much easier to understand than the discrete-logarithm problem, understanding how exactly it can be used to realize a public-key cryptosystem requires a bit of math (again). We start by defining an odd-looking function.
7.7.1 Euler’s totient function
No doubt you are familiar with prime numbers. To recap, p is a prime number if it has no divisors other than 1 and p. For two integer numbers a and b, we can always find a greatest common divisor c, or c = gcd(a,b) for short. c is the greatest integer that divides both a and b. For example, 3 is the greatest common divisor of 42 and 15, so we can write 3 = gcd(42,15). We can systematically find greatest common divisors with Euclid’s algorithm. Here is how it works for a = 42 and b = 15:
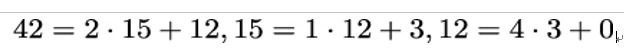
We start with an integer division of a by b with remainder r. In the next steps, the numbers change roles and the remainders become the new divisors, while the divisors become the new dividends. The algorithm stops if a remainder 0 is reached, which always happens at some point. The GCD is the remainder r occuring in the previous step – in this case, 3. Let’s look at another example, a = 35 and b = 9:
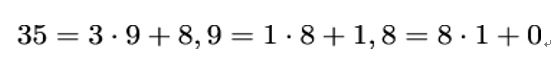
Here, we get gcd(35,9) = 1, which means 35 and 9 do not share any common factors except 1. Such numbers are called coprime.
Euler’s totient function is a function φ : ℕ →ℕ that counts for any input n how many numbers x < n are coprime to n, which means how many x < n there are with gcd(x,n) = 1. For example, there are 5 numbers smaller than 12 that are coprime to 12, namely 1, 3, 5, 7, and 11. So φ(12) = 5.
In general, in order to find ϕ(n) for some given n, we need the prime factorization of n, which means its unique decomposition into powers of prime numbers:
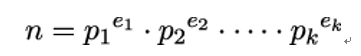
Finding the prime factors of a given integer number n is called the factorization problem. In the easiest case, n = p is a prime number itself. As a prime number, p does not have any divisors. So all numbers < p are coprime to p, which means
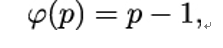
if p is a prime. The next (and for us most important) case is when n is a product of two primes p and p: n = p ⋅ q. Now there are q − 1 multiples of p that are not coprime to n, and p − 1 multiples of q that are not coprime to n. So the overall number of coprime numbers < n is:
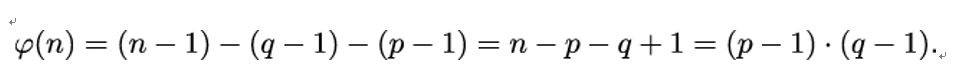
We are now ready to state the most important tool in the formulation of the RSA algorithm.
Euler’s theorem
Let m be coprime to n. Then
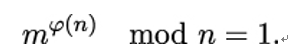
For example, φ(35) = 6 ⋅ 4 = 24, so according to Euler, 224 mod 35 = 1. Indeed, 224 = 16,777,216 = 479,349 × 35 + 1.
Leave a Reply