
7.7.3 The encryption function
In order to send an encrypted message to Alice, Bob needs to obtain an authentic copy of Alice’s public key PKAlice = (e,n). He then needs to encode his message m so that it fits into the plaintext space ℳ = {1,…,n− 1}. The ciphertext space 𝒞 is the same as ℳ. The encryption function ePK : ℳ→𝒞 works like this:
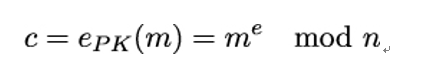
Encryption example
Let’s assume Bob wants to send the message m = 2 to Alice. He retrieves Alice’s public key PKAlice = (17,77) from the key pair generation example and computes
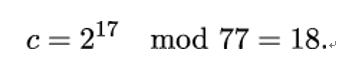
In general, Bob needs to compute powers of m for very large exponents e. There is an efficient algorithm for computing powers modulo n called Square and Multiply. It is based on the binary representation of e. Let the encryption exponent e consist of b bits:
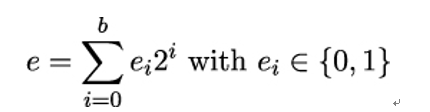
Then we have

The powers m2i can be computed by repeated squaring of m, because
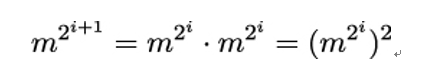
In order to get me, the squares m2i need to be multiplied, but only those where ei = 1. Thus, fewer 1-bits in the binary representation of e mean less computational effort for Bob. Let’s check the value given above for c = 217 mod 77 by re-computing it using the Square and Multiply algorithm (all values are given modulo 77):
- Square:
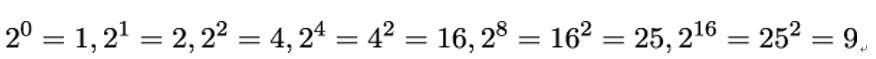
- Multiply:
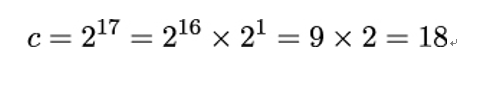
7.7.4 The decryption function
So Alice gets c = me mod n from Bob. How can she recover the plaintext? The decryption function dSK : 𝒞→ℳ works like this:
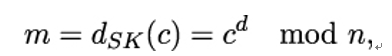
where d is Alice’s secret key. Why does this work? We have
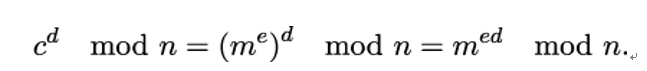
Remember that d was computed by Alice in such a way that ed mod φ(n) = 1. Equivalently, we know that there is some integer k so that
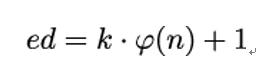
Using this expression as exponent, we get the following because of Euler’s theorem:
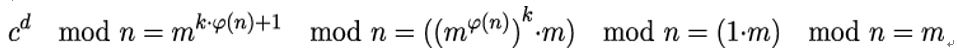
Note that in order to compute cd mod n, Alice can use the Square and Multiply algorithm described above. However, she has to use her private key d as exponent. In contrast to the encryption exponent e, she cannot control the number of ones in the binary representation of d. Therefore, decryption operations or generally operations that involve the private key are computationally more expensive than public key operations in RSA.
Let’s continue our earlier example with Alice decrypting the cipher c:
Decryption example:
Alice gets c = 18 from Bob. Using her private key SKAlice = 53, she computes
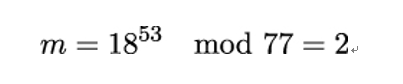
Leave a Reply