The discrete logarithm problem – Public-Key Cryptography

7.2.2 The discrete logarithm problem

If g is an element of a group 𝔾 with operation ⋆, we can define powers of g by writing

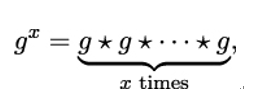
where g0 is defined to be the neutral element e.

The group 𝔽p∗ has a special property: it is cyclic, which means we can always find some number g ∈{1,2,…,p − 1} so that all other elements in 𝔽p∗ can be written as powers of g. For example, take p = 7 and g = 3. Then 31 = 3,32 = 2,33 = 6,34 = 4,35 = 5,36 = 1.

The number g is called a generator or primitive element of the cyclic group 𝔾. One can show that gn = e, when n is the order of G. In 𝔽p∗, the primality of p guarantees there is always a generator g ∈𝔽p∗ (actually, there are quite a lot of them), and we have gp−1 mod p = 1.

With these preliminaries, we are ready to formulate the discrete logarithm problem:

• Given: A group 𝔾 = (M,⋆), A ∈ M,g ∈ M
• Sought: A positive integer number x so that A = gx x is called the discrete logarithm of A to base g

For example, in 𝔽11∗, x = 4 is the discrete logarithm of A = 5 to base g = 2, because 24 mod 11 = 5. Note that if g is a generator, the discrete logarithm problem always has a solution (that is, for all A ∈ M). Therefore, the discrete logarithm problem is often formulated with the assumption that 𝔾 is a cyclic group and g is a generator of 𝔾, but this is not strictly necessary.

In some groups (including 𝔽p∗), the discrete logarithm problem is a hard problem. How hard it is exactly depends on the nature of the group operation ⋆. Consider, for example, the group 𝔾 = ({0,1,…,n − 1} with addition modulo n as the group operation. Then the discrete logarithm problem of finding a value for x so that gx = A reduces to g ⋅ x = A. So, all we have to do is to find the multiplicative inverse of g modulo n (which can be done by using the extended Euclidean algorithm – see Section 7.7, The RSA algorithm, in this chapter for details) and multiply it by A to get x = g−1 ⋅ A.

The fastest generic algorithms (that is, algorithms that do not use special properties of the group operation) for finding the discrete logarithm in a group of prime order p are the baby-step giant-step algorithm and Pollard’s rho algorithm (see Section 8.4, Security of elliptic curves for details). These algorithms have a running time in O(), which is exponential in the bit length of p.

Another algorithm, the Pohlig-Hellman algorithm, is able to reduce the discrete logarithm problem in cyclic groups of composite order n = p1e1p2e2…pses to s distinct problems in subgroups of prime order pi. This is actually quite important, because the group order of 𝔽p∗ is p− 1, which is never prime! So, it is not sufficient just to choose a large prime p; we also have to take care that p − 1 does not have many small prime factors. For example, some prime numbers p are of the form p = 2q + 1, with q being another prime. In this case, the prime factors of p − 1 are 2 and q, and Pohlig-Hellman reduces the difficulty of the discrete logarithm problem by a factor of 2 only. For this reason, prime numbers of the form p = 2q + 1 are called safe primes.

Unfortunately, 𝔽p∗ is not a generic group. There are even faster algorithms for finding discrete logarithms, for example, the index-calculus method, which works especially well in 𝔽p∗ and has a sub-exponential running time in the bit length of p. However, if the bit length of p is larger than 2,048 bits, then the discrete logarithm problem in 𝔽p∗ is still considered to be hard.

The discrete logarithm problem can be seen as the inverse problem of computing powers of g, which only involves repeated applications of the group operation ⋆. So, as long as we are working in a group where the discrete logarithm problem is hard, we have a first example of a trapdoor function. In the next section, we will see how this can be used to exchange a secret key over an insecure channel.