
7.10.2 Supported groups
When client Bob starts a TLS handshake with server Alice and wishes to use the ECDHE or DHE key agreement protocol, he transmits the supported˙groups extension listing the named groups that Bob supports. The groups are listed in the order of most to least preferred.
The extension˙data field of supported˙groups contains the value NamedGroupList as defined in Listing 7.3. The Elliptic Curve Groups (ECDHE) are the names of elliptic curves supported by the TLS 1.3 standard. These elliptic curves are defined in FIPS 186-4 and RFC 7748.
Listing 7.3: Named finite fields and elliptic curves supported in TLS 1.3
enum {
/* Elliptic Curve Groups (ECDHE) */
secp256r1(0x0017), secp384r1(0x0018), secp521r1(0x0019),
x25519(0x001D), x448(0x001E),
/* Finite Field Groups (DHE) */
ffdhe2048(0x0100), ffdhe3072(0x0101), ffdhe4096(0x0102),
ffdhe6144(0x0103), ffdhe8192(0x0104),
/* Reserved Code Points */
ffdhe_private_use(0x01FC..0x01FF),
ecdhe_private_use(0xFE00..0xFEFF),
(0xFFFF)
} NamedGroup;
struct {
NamedGroup named_group_list<2..2^16-1>;
} NamedGroupList;
Similarly, Finite Field Groups Diffie-Hellman (DHE) contains the list of finite fields that client Bob and server Alice can use in Diffie-Hellman key agreement as an alternative to elliptic curve groups in the TLS 1.3 handshake. These fields are defined in RFC7919. Finally, the Reserved Code Points is a placeholder for private use as defined in RFC8126.
If Alice and Bob use the Diffie-Hellman Ephemeral (DHE) key agreement, client Bob sends server Alice a list of finite field groups that Bob supports. Alice picks one specific group out of that list. Her choice determines the finite field generator g and modulus p.
For the finite field-based Diffie-Hellman key agreement to be secure, Alice and Bob must choose secure cryptographic parameters. As an example, it has been shown [117] that the use of small private exponents with a random prime modulus p renders the computation of the discrete logarithm easy. For this reason, having a definition of suitable finite field groups is crucial.
All primes in the finite field groups used in TLS 1.3 are so-called safe primes. As discussed in Section 7.2, Groups a safe prime p has the form p = 2q + 1 where q is also a prime.
In practice, private Diffie-Hellman exponents are usually chosen independently and uniformly at random from {0,…,p − 2}. When p is a safe prime, the most probable Diffie-Hellman key is only 6 times more likely than the least probable and the key’s entropy is only 2 bits less than the maximum lg(p − 1) [117].
With e denoting the base of the natural logarithm and ⌊…⌋ denoting the floor operation, the finite field groups defined in RFC 7919 and used in TLS 1.3 are derived for a given bit length b by finding the smallest positive integer x that creates a safe prime p of the form:
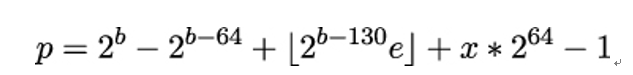
As an example, the 2,048-bit finite field group ffdhe2048 is calculated as follows. The modulus equals to:
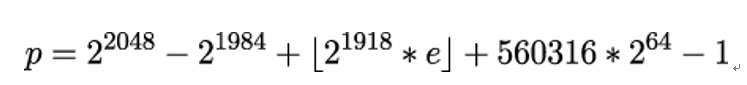
The modulus’ p hexadecimal representation is:
FFFFFFFF FFFFFFFF ADF85458 A2BB4A9A AFDC5620 273D3CF1
D8B9C583 CE2D3695 A9E13641 146433FB CC939DCE 249B3EF9
7D2FE363 630C75D8 F681B202 AEC4617A D3DF1ED5 D5FD6561
2433F51F 5F066ED0 85636555 3DED1AF3 B557135E 7F57C935
984F0C70 E0E68B77 E2A689DA F3EFE872 1DF158A1 36ADE735
30ACCA4F 483A797A BC0AB182 B324FB61 D108A94B B2C8E3FB
B96ADAB7 60D7F468 1D4F42A3 DE394DF4 AE56EDE7 6372BB19
0B07A7C8 EE0A6D70 9E02FCE1 CDF7E2EC C03404CD 28342F61
9172FE9C E98583FF 8E4F1232 EEF28183 C3FE3B1B 4C6FAD73
3BB5FCBC 2EC22005 C58EF183 7D1683B2 C6F34A26 C1B2EFFA
886B4238 61285C97 FFFFFFFF FFFFFFFF
The generator g equals 2, and the group has the size q = (p − 1)∕2. The hexadecimal representation of q is:
7FFFFFFF FFFFFFFF D6FC2A2C 515DA54D 57EE2B10 139E9E78
EC5CE2C1 E7169B4A D4F09B20 8A3219FD E649CEE7 124D9F7C
BE97F1B1 B1863AEC 7B40D901 576230BD 69EF8F6A EAFEB2B0
9219FA8F AF833768 42B1B2AA 9EF68D79 DAAB89AF 3FABE49A
CC278638 707345BB F15344ED 79F7F439 0EF8AC50 9B56F39A
98566527 A41D3CBD 5E0558C1 59927DB0 E88454A5 D96471FD
DCB56D5B B06BFA34 0EA7A151 EF1CA6FA 572B76F3 B1B95D8C
8583D3E4 770536B8 4F017E70 E6FBF176 601A0266 941A17B0
C8B97F4E 74C2C1FF C7278919 777940C1 E1FF1D8D A637D6B9
9DDAFE5E 17611002 E2C778C1 BE8B41D9 6379A513 60D977FD
4435A11C 30942E4B FFFFFFFF FFFFFFFF
The ffdhe2048 finite field group has an estimated security strength (based on the strength of symmetric key cryptographic primitives) of about 100 bits.
Keeping in mind the mathematical fundamentals of public-key cryptography we discussed earlier in this chapter, you might have spotted a small inconsistency in the TLS 1.3 specification language. The specification talks about elliptic curve groups and finite field groups. But we, of course, know that any field is automatically a group and that all elliptic curves are groups by definition.
In TLS 1.3, server Alice can send the supported˙groups extension to client Bob. However, Bob is not allowed to act upon any data in supported˙groups before he successfully completes the handshake with Alice. Bob may only use this information to adjust the list of named groups in his key˙share extension in subsequent TLS sessions with Alice.
If server Alice has a group she prefers to those sent by client Bob in his key˙share extension but is still willing to accept Bob’s ClientHello message, she sends a supported˙groups extension to communicate to Bob her preferences. Moreover, that extension lists all groups that Alice supports, even if some of them are currently unsupported by client Bob.
Leave a Reply