7.8 Security of the RSA algorithm

The security of the RSA algorithm relies on the following three assumptions:

• The factoring problem is hard for the given public modulus n
• The RSA problem is hard
• The public keys of Alice and Bob are authentic

We will discuss each of these assumptions in turn.

7.8.1 The factoring problem

If an attacker manages to compute the two prime factors p and q of the public modulus n, they can repeat the steps taken by Alice when she computed her key pair. In particular, an attacker could compute Alice’s secret key and compromise the whole system. Therefore, the security of the RSA cryptosystem is crucially based on the intractability of the integer factorization problem, which is in general defined as follows:

Given a positive integer n, find its prime factors p1 to pk such that

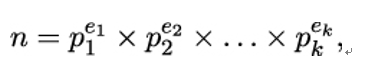
where pi are pairwise distinct primes.

The fastest algorithm to factorize semiprimes, which are numbers of the form n = p ⋅ q with p and q primes of approximately equal size, currently known is called the Number Field Sieve ([82], section 3.7.3). It has a subexponential (but not polynomial) running time in the bitlength of n.

Using the Number Field Sieve, the largest semiprime yet factored was RSA-240, a 795-bit number with 240 decimal digits, in February 2020 [38]. Therefore, public moduli with 1,024 bits, which were quite common in the past, cannot be considered secure anymore and should no longer be used. The American standardization authority NIST has compiled the following table of key lengths of comparable security strength for symmetric block ciphers (see Chapter 14, Block Ciphers and Their Modes of Operation) and asymmetric algorithms [126].

Security strength (bits)	Block cipher	Length of RSA modulus n	Length of prime p in DH over 𝔽p∗
≤ 80	2-Key 3DES	1024	1024
112	3-Key 3DES	2048	2048
128	AES-128	3072	3072
192	AES-192	7680	7680
256	AES-256	15360	15360

 Table 7.3: Equivalent key lengths of symmetric and asymmmetric algorithms

Note that a security strength of 80 bits is no longer considered adequate. We will amend Table 7.3 in the next chapter with the corresponding numbers for Diffie-Hellman over elliptic curves.

7.8.2 The RSA problem

The RSA problem concerns the security of the RSA encryption function. If Eve knows the public key of Alice, PKAlice = (e,n), and observes the cipher c = me mod n, we ask whether Eve can find m without knowing the secret key SKAlice = d.

More formally, the RSA problem is defined as follows:

• Given: A positive integer n = p⋅q that is a product of two distinct odd primes p and q, a positive integer e such that gcd(e,(p−1)(q−1)) = 1, and an integer c < n
• Sought: An integer m < n such that me = c (mod n)

This problem can be summarized as the problem of finding e−th roots modulo n. In general, if Eve manages to factorize n, she can compute the secret key d and compute m via m = cd mod n. This is currently considered to be the fastest way to solve the RSA problem in general cases, so the difficulty of the RSA problem is closely tied to the integer factorization problem.

Therefore, the relation of the RSA problem to the factorization problem parallels the relation of the Diffie-Hellman problem to discrete logarithm problems.

There are, however, some special cases of the RSA problem that might go wrong. If the encryption exponent e chosen is very small, it might happen that me mod n = me, that is, there is no wrap-around n and the RSA problem reduces to take an ordinary e−th root. In a similar vein, problems can arise if the same message m is enciphered with the public keys of r receivers, where each receiver uses the same e, but different moduli ni. If Eve observes the r ciphers

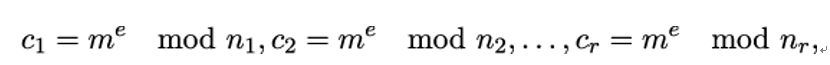
she can compute a number c with

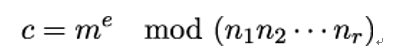
using the Chinese Remainder Theorem (CRT) (see e.g. [82], Theorem 2.25). Again, if there is no wraparound, m can be found by taking the ordinary e−th root of c. This is called the Small Exponent Attack on RSA. In practice, this issue is prevented by randomly padding each message before encryption.