8.4 Security of elliptic curves

The security of cryptographic mechanisms based on elliptic curves relies on the following assumptions:

• The elliptic curve discrete logarithm problem is computationally hard for the chosen elliptic curve
• The chosen elliptic curve has no mathematical backdoors
• Alice’s and Bob’s public keys are authentic
• In the case of ECDH, the Diffie-Hellman problem is computationally hard in the cyclic group 𝔾 generated by the base point G on the elliptic curve

In Chapter 7, Public-Key Cryptography, we already discussed – both for Diffie-Hellman key exchange as well as the RSA algorithm – why it is important for Alice’s and Bob’s public keys to be authentic. We also explained why the Diffie-Hellman problem must be computationally hard for the key agreement to be secure.

In this chapter, we will discuss how to fulfill the first two assumptions. We’ll start by looking at the available algorithms for determining discrete logarithms over elliptic curves.

8.4.1 Generic algorithms for finding discrete logarithms

The naive algorithm for solving ECDLP computes 2G,3G,4G,… all the way up to n, the order of the cyclic group 𝔾 and compares the elements of this list to the term kG. Obviously, the algorithm requires 𝕆(n) steps.

A much faster approach to solving ECDLP involves so-called collision algorithms that leverage the birthday paradoxon. This is a phenomenon known from probability theory that refers to the fact that it is easier to find collisions than specific elements in a set. As a result, these algorithms reduce the number of required steps from 𝕆(n) to 𝕆() [166].

To give you an idea how collision algorithms work, we will now describe two such algorithms, the Babystep-Giantstep algorithm and Pollard’s Rho algorithm. We have deliberately left out the more subtle mathematical details. If you want to completely understand the mathematics behind these algorithms, [166] is a good source of information.

Shanks’ babystep-giantstep algorithm

Let G be a base point on an elliptic curve E and 𝔾 be a cyclic group of order n generated by G. Further, let P be an element of 𝔾. That is, P = kG. The babystep-giantstep algorithm proposed by the American mathematician Daniel Shanks finds the unique integer k and, thus, solves ECDLP as follows:

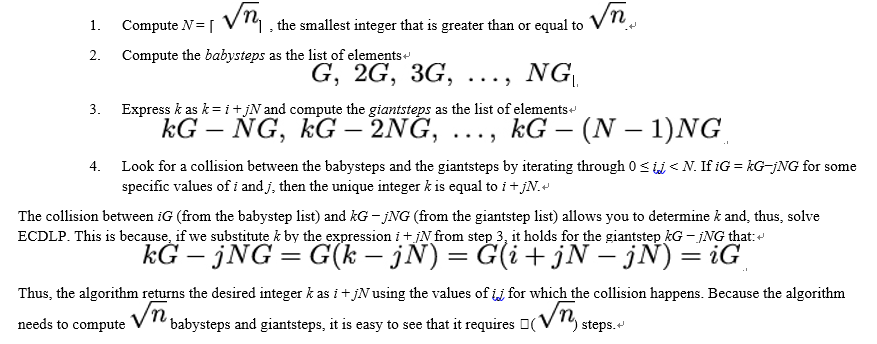
Pollard’s ρ algorithm

This algorithm for solving the discrete logarithm problem was proposed in 1978 by the British mathematician John Pollard. With a slight modification, it can also be used to solve ECDLP.

As with the previous algorithm, let G be a base point on an elliptic curve E and 𝔾 be a cyclic group of order n generated by G. Further, let P = kG with some unknown k.

Pollard’s ρ algorithm finds k and, therefore, solves ECDLP as follows:

1. Split the group 𝔾 into three sets of roughly the same size and select a random mapping f : 𝔾 →𝔾. If the mapping f : 𝔾 →𝔾 is sufficiently random, one can prove that a collision should be expected after  elements where n is the order of group 𝔾 (see, for instance, [166] for detailed mathematical proof).
2. Using step 1, find numbers a, b, c, and d such that:

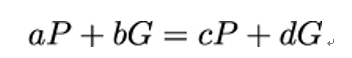
3. Once these numbers – that is, the collision – are found, rewrite the preceding equation as:

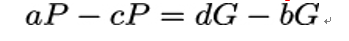
which is equivalent to:

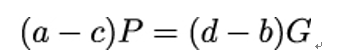
and, since P = kG, can be rewritten as:

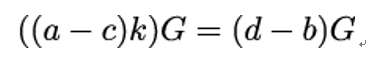
4. Based on the preceding equation, observe that (a−c)k = (d−b) (mod n). Therefore, k = (d − b)(a − c)−1.

Like Shanks’ algorithm, Pollard’s ρ algorithm requires 𝕆() steps. Both algorithms are generic in the sense that they can be applied to the discrete logarithm problem in any group, that is, they do not use any special properties of elliptic curves. Here lies the real advantage of working with elliptic curves compared to other, less abstract groups such as 𝔽p∗. Apart from some special cases, there are no known shortcuts for computing discrete logarithms in elliptic curves. We’ll now look at these special cases.