Projective coordinates – Elliptic Curves

8.1.3 Projective coordinates

In order to get to grips with the mysterious point at infinity O, we need to extend the set of points that satisfy y2 = x3 + ax + b. We can do so by introducing yet another set of coordinates. Let 𝔽 be a field. We look at triples (X,Y,Z), where X,Y,Z are from 𝔽 and are not all zero at the same time. This looks like some three-dimensional space 𝔽3 without the origin, but we are only interested in lines through the origin, not at the single points, so we consider all points in 𝔽3 ∖{0,0,0} to be equivalent, if they lie on the same line through the origin. More precisely, we say that the triple (X1,Y 1,Z1) is equivalent to (X2,Y 2,Z2) if there is some factor λ ∈𝔽 so that

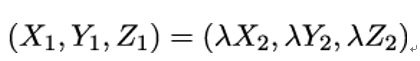
The set of all equivalent triples (X,Y,Z) is called an equivalence class. Each equivalence class is called a projective point, and all projective points taken together form the projective plane.

The points of the ordinary or affine plane 𝔽2 can be mapped onto points of the projective plane: the affine point (x,y) corresponds to the projective point (x,y,1). Similarly, for Z≠0 , the projective point (X,Y,Z) is equivalent to (X∕Z,Y∕Z,1), which can be identified with the affine point (X∕Z,Y∕Z). This means, for Z≠0, there is a one-to-one correspondence between points of the affine plane and points of the projective plane. The projective points with Z = 0, however, do not have an equivalent in the affine plane. They can be thought of as adding a kind of horizon to the affine plane, that is infinitely far away.

What happens if we use projective coordinates (X∕Z,Y∕Z) instead of the ordinary (x,y) in our equation for E? We get

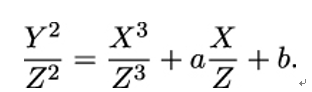
Multiplying both sides by Z3 to get rid of the denominators gives us

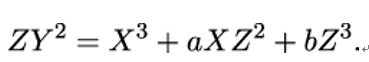
Note that in this polynomial equation, all terms have the same overall degree 3. Polynomials of this form are called homogeneous. This homogeneous polynomial represents the projective version of the elliptic curve. It is satisfied by a projective point (X,Y,Z) with Z≠0 if and only if the corresponding affine point (x,y) = (X∕Z,Y∕Z) satisfies y2 = x3 + ax + b. But what about the projective points with Z = 0? Plugging Z = 0 into the projective equation, we get

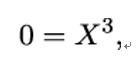
so X must be zero as well. But there is no restriction on Y apart from being non-zero, so we can choose Y = 1 and get another projective point O = (0,1,0) as the solution of the projective equation. This point does not have an equivalent in the affine plane, but it can be visualized as lying on the infinitely far away end of the y axis.

Apart from providing a formal justification for having an additional point O at infinity on our elliptic curve, the use of projective coordinates is also more efficient when doing calculations on elliptic curves. We will return to this issue shortly when discussing the addition law for points on an elliptic curve.