Key pair generation – Public-Key Cryptography

7.7.2 Key pair generation

Alice generates her RSA key pair with the following steps:

1. Generate two large primes p and q of about equal size. Compute their product n = p ⋅ q and φ(n) = (p − 1) ⋅ (q − 1). n is called the public modulus.
2. Choose a number e > 1 that is coprime to φ(n). e is called the encryption exponent.
3. Compute a number d with (e ⋅ d) mod φ(n) = 1, which means: find the multiplicative inverse of e modulo φ(n).
4. Publish the pair

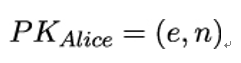
as a public key. Keep the number

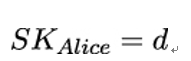
secret, along with p,q, and φ(n).

There are a few things in this recipe we need to discuss before we move on to an example:

• How does Alice generate prime numbers of suitable length? She first generates a random number of the required length and then tests it for primality. The mathematical basis for these tests is an easy consequence of Euler’s theorem:

Fermat’s little theorem

Let p be a prime number. Then, for all a < p,

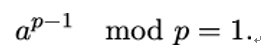
To test whether the number p is prime, we can check if a randomly chosen a satisfies Fermat’s little theorem. This is called the Fermat primality test [109]. If ap−1 mod p≠1, we can be sure that p is not prime. However, if ap−1 mod p = 1, we cannot be sure that p is prime, as Fermat’s little theorem is only a necessary condition for primality. Luckily, there is a refinement of the Fermat test called the Miller-Rabin test. It can be shown that if the Miller-Rabin test is successfully repeated t times with different numbers a < p, the probability of p being a prime is at least 1 − 2−t (see [177], Theorem 3.18).

• Is there any danger of two people independently generating the same prime numbers? You probably know the ancient theorem by Euclid that states that there are infinitely many prime numbers. OK, but what if they are very thinly spread out in the large number regions that interest us?

We can deal with this issue by stating another important theorem from the late 19th century:

Prime number theorem

Let π(N) be the number of prime numbers that are smaller than N. Then

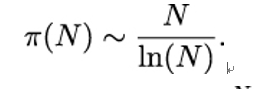
The ∼ symbol means that as N grows toward infinity, the two functions π(N) and  grow in a similar way, or, to put it more technically,

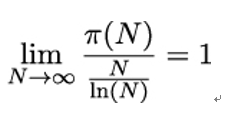
We can use the prime number theorem to roughly estimate the number of primes with a given size, for example, 1,024 bits. That’s the number of primes between N1 = 21024 and N2 = 21023, which is

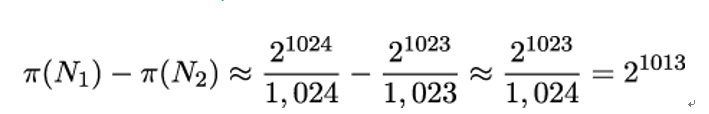
• How can Alice find a number d so that ed mod φ(n) = 1? For this, she can use an extension of Euclid’s algorithm. Remember Euclid’s algorithm computes the greatest common divisor of two input numbers a and b. Alice now applies Euclid’s algorithm to e and (p − 1)(q − 1), with the obvious result 1, because she has chosen e to be coprime to φ(n). She then goes backward through Euclid’s algorithm with the aim of finding a linear combination of e and φ(n) that equals 1:

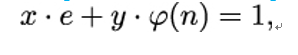
with x and y being integer numbers.

How this backtracking works exactly can be understood best when looking at the key pair generation example that follows. We can rewrite the linear combination in the form

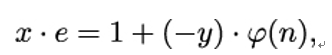
and this shows us that we have found a number x with (xe) mod φ(n) = 1. Therefore, the number x is the secret key d Alice is looking for. If x happens to be negative, we can make it a positive number by adding φ(n), which is the same as adding 0 modulo φ(n).

Now let’s look at a toy Example for RSA key generation:

• Alice chooses p = 7 and q = 11 as prime numbers. Then n = 7⋅11 = 77 and φ(n) = 6 ⋅ 10 = 60.
• As encryption exponent, Alice chooses e = 17.
• Alice now needs to compute a number d so that 17d mod 60 = 1. She applies Euclid’s algorithm to 60 and 17 until she reaches 1 as the remainder:

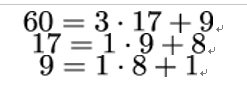
Now she solves these equations for the last remainder 1, starting with the last equation and successively replacing the other two remainders with their representation from the other equations:

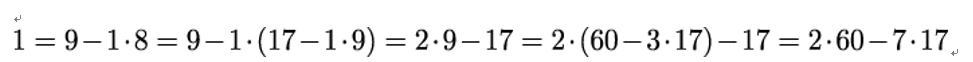
The factor of 17 in this linear combination is -7, which is the same as 53 mod 60. Indeed, we have

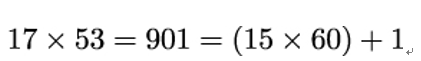
So Alice sets d = 53 as her secret key.

• Alice publishes PKAlice = (17,77) and keeps SKAlice = 53 secret.

Alice has chosen e = 17 as her encryption exponent because the binary representation of 17 has few bits that are equal to 1. This makes it easier for Bob to encrypt messages for her, as we will see in the next subsection.