7.10.3 Finite Field Diffie-Hellman in TLS

When finite field groups are used, server Alice and client Bob execute the conventional Diffie-Hellman key agreement protocol as described in Figure 7.2. The secret Alice and Bob agree upon is converted into a byte string by encoding it in big-endian form and left-padding it with zeros up to the size of the prime. This converted byte string forms the Handshake Secret SH, which is subsequently used as the shared Diffie-Hellman ephemeral secret in the TLS key schedule to further derive the client˙handshake˙traffic˙secret (CHTS), the server˙handshake˙traffic˙secret (SHTS), the derived˙handshake˙secret (dHS), and finally the master˙secret (MS) (see Section 12.3, KDFs in TLS).

7.11 Hybrid cryptosystems

From the previous sections, you might have got the (correct) impression that using a public-key cryptosystem is rather costly in terms of computation time. For example, according to [177], p. 121 key generation in the RSA cryptosystem has an effort in O(ℓ4 log(ℓ)), where ℓ is the bitlength of the public modulus n, and encryption or decryption of an n-bit plaintext block takes O(n3 bit operations. Such an effort is unacceptable for the encryption of large amounts of data.

Therefore, most cryptographic systems used in practice today are hybrid cryptosystems. Hybrid cryptosystems combine the advantage of public-key cryptography of being able to bootstrap a secure communication channel to a previously unknown communicating party with the speed and efficiency of symmetric-key encryption, decryption, and hashing operations [188].

7.11.1 High-level description of hybrid cryptosystems

Figure 7.6 illustrates the basic architecture and the fundamental working principle of hybrid cryptosystems. A hybrid cryptosystem is composed of two separate cryptographic systems:

• A public-key cryptosystem PKS used as a secure means for the communicating parties Alice and Bob to establish a shared secret
• A symmetric-key cryptosystem SKS used to secure the actual (bulk) data by transforming it using a desired cryptographic operation.

A hybrid cryptosystem works by Alice and Bob first establishing a shared secret key k using a public-key cryptosystem PKS and mathematically verifiable credentials.

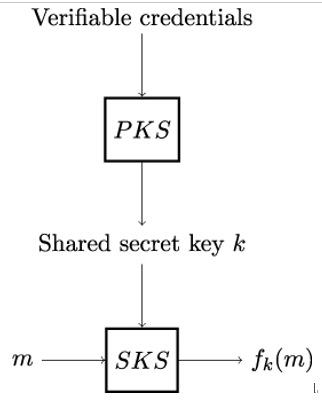
Figure 7.6: Working principle of a hybrid cryptosystem

We will have much more to say about how the verifiable credentials work in detail in Chapter 10, Digital Certificates and Certification Authorities. For now, it is sufficient to know that these credentials are constructed in such way that Alice can verify Bob’s identity and Bob can verify Alice’s identity. Or, more precisely, Alice can verify that the other communicating party claiming to be Bob is indeed Bob, and vice versa.

Most importantly, Alice and Bob can verify each other’s identity even if they have never met before. This works by having a third party that both Alice and Bob trust – let’s call him Trent – vouch for Bob’s and Alice’s identities in advance. This act of vouching is encoded in the credentials so that Alice and Bob can perform the identity verification of the other party without the need to communicate with Trent.

Conceptually, the ability of communicating parties that never met before to verify each other’s identities without the online, real-time support of a trusted third party solves the key distribution problem. In other words, public-key cryptography relieves Alice and Bob from having to share a common secret in advance.

In the second step, having established a shared secret key k, Alice and Bob use a symmetric-key cryptosystem SKS to compute a desired cryptographic function fk(m) on the bulk payload data m they want to secure.

Compared to public-key cryptographic schemes, symmetric-key schemes are orders of magnitude faster and much easier to implement because, unlike public cryptography, they do not require arbitrary-precision arithmetic where calculations are performed on huge numbers having hundreds of digits and limited only by the amount of working memory available in the computer.

As a result, cryptographic computations on large bulk data, for example, an audio or video stream of several gigabytes, can be done very efficiently and at high speed using a symmetric-key cryptosystem SKS.