Explicit formulae – Elliptic Curves

8.2.2 Explicit formulae

The geometrical viewpoint is nice to get an intuitive picture of point addition, but in order to actually implement things on a computer we need to have explicit formulae telling it what to do. Moreover, the geometrical picture is not valid anymore if we work in a finite field. Still, we can use the well-known tools from calculus and analytic geometry over real numbers to get explicit expressions for secants, tangents, intersection points, and so on, and finally, for the sum of points and point doubling on an elliptic curve. With a few small modifications, these formulae then carry over to finite fields. This is what you get for real, affine coordinates.

Let P = (x1,y1) and Q = (x2,y2) be points on a smooth elliptic curve in reduced Weierstrass form: E : y2 = x3 + ax + b. Let’s add and double these points:

• Point Addition: Let R = P + Q. The coordinates (x3,y3) of R are given by:

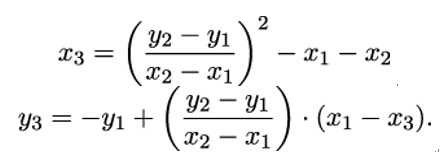
• Point Doubling: Let R = P + P = 2P. The coordinates (x3,y3) of R are given by:

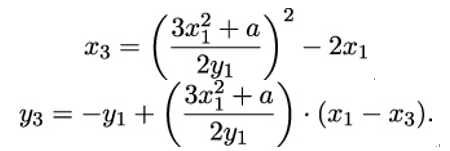
Take, for example, the curve E : y2 = x3 − 4x + 1 and the points P = (0,1),Q = (3,4). Then  = 1 and

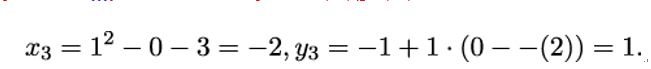
So R = P + Q = (−2,1). Similarly, we get 2P = P + P = (4,7).

The computationally most expensive part of the formulae above are the divisions, especially when carried out in a finite field 𝔽p, where division by x really means multiplication by x−1 mod p. We can save a lot of this effort, if we translate our formulae into projective coordinates, that is, by replacing P = (x1,y1) and Q = (x2,y2) with their projective counterparts (X1∕Z1,Y 1∕Z1,1) and (X2∕Z2,Y 2∕Z2,1). After a lot of algebra and a final multiplication to get rid of all denominators, the final result is (see [141]):

• Point Addition We set U = X1Z2 − X2Z1, T = Y 1Z2 − Y 2Z1 and W = T2Z1Z2 − U2(X1Z2 + X2Z1). With these abbreviations, we get

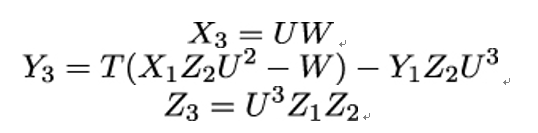
• Point Doubling We set T = 3X12 + aZ12. With this abbreviation, we get

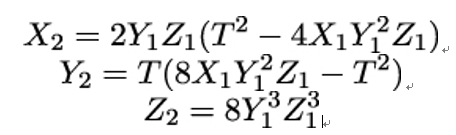
Basically, we are trading a lot of multiplications and additions against the divisions in the affine case. The transfer back to affine coordinates is done by a single division, namely dividing all coordinates by the Z-coordinate value.