8.3 Elliptic curves over finite fields

Now let’s see what elliptic curves over finite fields look like. As we established in the last chapter, there are only two kinds of finite fields: 𝔽p = {0,1,2,…,p − 1}, where p is a prime number, and 𝔽p[X]∕M, where p is a prime number and M is an irreducible polynomial of degree n with coeffcients ai ∈𝔽p. The essential difference between the two is that 𝔽p has p elements, whereas 𝔽p[X]∕M has pn elements. For this reason, 𝔽p[X]∕M is often called 𝔽pn without explicitly stating the polynomial M.

8.3.1 Elliptic curves over 𝔽p

We focus on the case p > 3, so that char(𝔽p) > 3. Then it is always possible to generate the reduced Weierstrass form of the curve, and we can use the following definition.

Elliptic curve over 𝔽p

Let p > 3 be a prime number. An elliptic curve over 𝔽p is the set of points (x,y) satisfying

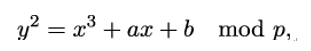
where x,y,a,b ∈𝔽p and Δ = 4a3 + 27b2≠0 mod p, together with some point O.

Note that here we have already included the smoothness condition in the very definition of an elliptic curve. What do these discrete elliptic curves look like? Figure 8.6 provides an example, where a = 5,b = 5, and p = 17.

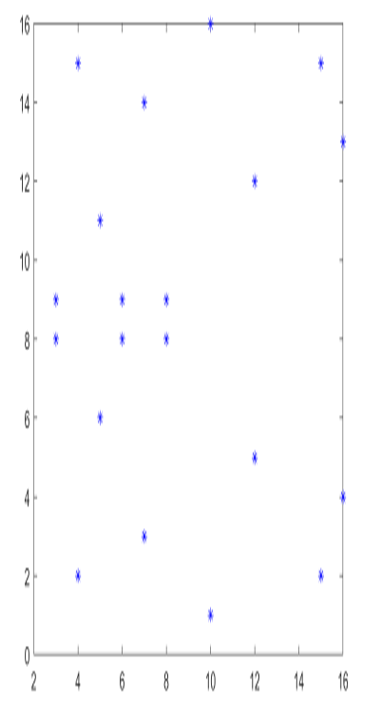
Figure 8.6: The curve E : y2 = x3 + 5x + 5 mod 17

This discrete set of points does not bear much resemblance to the smooth curves we have drawn over ℝ in the last section. Still, the explicit formulae for point addition and point doubling given in the last section magically carry over to 𝔽p. We only need to observe that all calculations are being done modulo p, and that division really means multiplication with an inverse modulo p. So all elliptic curves over 𝔽p defined in this way form an abelian group.

Recall from Chapter 7, Public-Key Cryptography that the number of elements of a group 𝔾 is called its order. So what is the order of an elliptic curve E over 𝔽p? By manually counting the points in Figure 8.6 (and not forgetting point O) we see that this special curve has 21 points. Unfortunately, there is no explicit formula giving us the number of points of an elliptic curve E in terms of a,b, and p, but we can try to estimate the number. An easy way to get an upper limit on the number of points is to assume that if we plug each possible x value from {0,1,…,p − 1} into the right-hand side of the curve equation, we get a perfect square modulo p every time. So each possible x value would provide two possible y values y1,2 = ±, which gives us an upper limit of 2p + 1 points (again, don’t forget the point O).

Using much more advanced mathematical tools, we can get a much better estimate. Hasse’s theorem (see [102], Chapter 6, Corollary 1.2) tells us that the number N of points of an elliptic curve E over 𝔽p lies between p + 1 − 2 and p + 1 + 2.

So the number of points on E over 𝔽p is quite close to p. This fact will become important a bit later, when we discuss the discrete logarithm problem on E.