8.2 Elliptic curves as abelian groups

Two points P and Q on a smooth elliptic curve E in reduced Weierstrass form can be added to give another point R = P + Q on E. The addition process can be best understood by describing it as a geometrical recipe over the real numbers first.

8.2.1 Geometrical viewpoint

To find the sum of two points P and Q on E, we draw a line through P and Q first. One can show that this line must have exactly one additional intersection point with E. We find this point and form the mirror image of it with respect to the x axis by reversing the sign of its y coordinate. The result is the sum P + Q. This process is visualized in Figure 8.3.

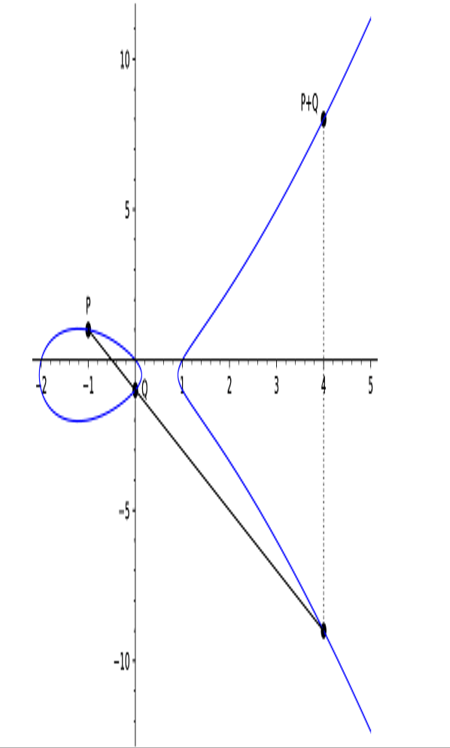
Figure 8.3: Elliptic curve point addition

Now let’s look at some special cases:

• If P = Q, we form the tangent line t to E at P, find its intersection point with E and reverse the sign of its y coordinate. The result is the point P + P = 2P (see Figure 8.4).

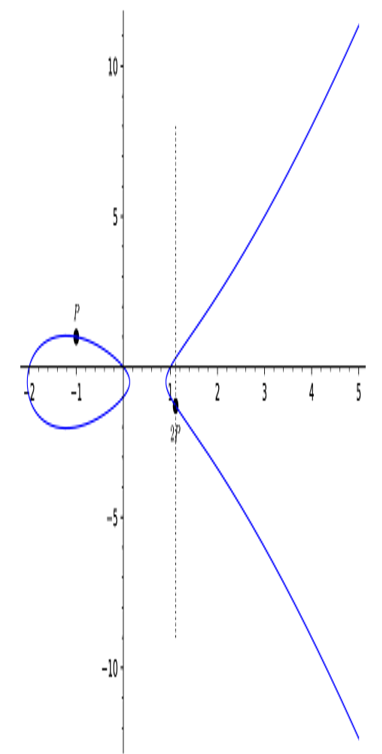
Figure 8.4: Point doubling on an elliptic curve

• If Q = O, we define P + O to be P. This means that O serves as a neutral element for the point addition.
• If P = (c,d) and Q = (c,−d) have the same x coordinate c, the line x = c joining them is vertical. It intersects E at the point at infinity O. This can be seen by writing x = c in projective coordinates x = X∕Z: we have X∕Z = c. Multiplying by Z gives us the projective version of the connecting line:

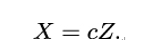
Clearly, the point O = (0,1,0) lies on this projective line. But we have already established that O also lies on the curve, so O must be the point of intersection.

Replacing Y by −Y in projective coordinates does not give a new point, so O is the final result of adding P and Q: (c,d) + (c,−d) = O. But this means that for a point P = (c,d) on E,

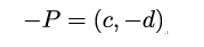
(see Figure 8.5).

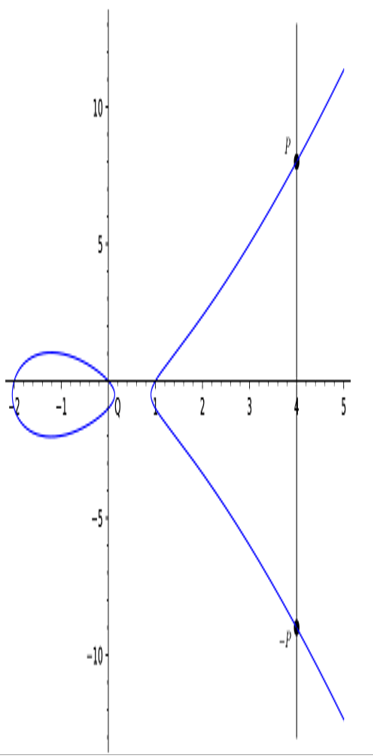
Figure 8.5: P + (−P) = O

Summing up, we have defined an operation + that maps a pair of points P and Q on E to their sum P + Q, which is also on E. The operation has O as a neutral element, and for a point P = (c,d) ∈ E, we can find its negative −P = (c,−d) ∈ E. It is also quite obvious that + is a commutative operation, because the order of P and Q does not affect the line joining them, so the end result of the adding process wil be the same. The only thing that remains to be checked before we can declare the pair (E,+) to be an abelian group is the associativity law for +, that is, we need to prove that

for any points P,Q,R on E. This turns out to be a bit tricky, but it can be proved by using tools from projective geometry (see [102], p. 120, for example).

Summing up, we have proved that a smooth elliptic curve E together with the point O at infinity forms an abelian group with respect to point addition as defined above.

More generally, the zeros of a set of polynomials is called an abelian variety, if a group law can be defined on them. Abelian varieties can be seen as the generalization of elliptic curves, but as yet they have not found any applications in cryptography.