Discrete logarithms and Diffie-Hellman key exchange protocol – Elliptic Curves

8.3.3 Discrete logarithms and Diffie-Hellman key exchange protocol

In Section 7.2, Groups, we defined the discrete logarithm problem for generic groups 𝔾. We repeat the definition here for convenience:

• Given: A group 𝔾 = (M,⋆), A ∈ M,g ∈ M
• Sought: A positive integer number n so that A = gn.n is called the discrete logarithm of A to base g.

The purpose of this section is to specialize this generic formulation to elliptic curve groups and to formulate the Diffie-Hellman key exchange protocol for elliptic curves.

Remember that in the earlier definition, gn is an abbreviation for g ⋆ g ⋆  ⋆ g, where the group operation ⋆ is applied n times. In an elliptic curve E, the group elements are points P ∈ E, and the group operation is an addition, traditionally written by a + – sign. This means that gn = g ⋆g ⋆⋆g becomes P + P +  + P = nP.

Now we can re-formulate the discrete logarithm problem for elliptic curves (ECDLP):

• Given: An elliptic curve E over 𝔽p, where p > 3, or over 𝔽2k. A point G ∈ E and a point P in the cyclic subgroup generated by G.
• Sought: A positive integer number n so that P = nG.n is called the discrete logarithm of P to base G.

We have added the requirement that P should be in the cyclic subgroup generated by G so that the ECDLP always has a solution.

Now, it is very easy to specialize the earlier generic formulation of the Diffie-Hellman key exchange protocol (see Figure 7.1) to elliptic curves:

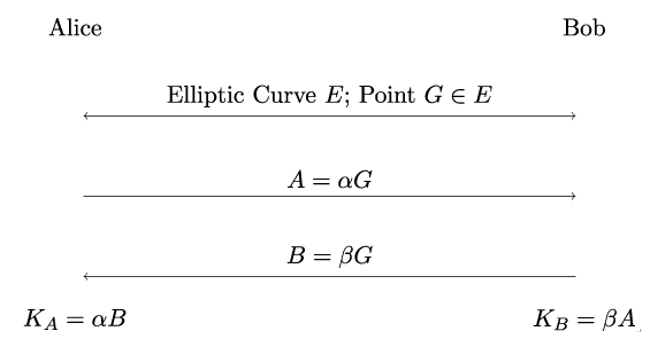
Figure 8.8: Diffie-Hellman key exchange protocol over an elliptic curve E

As in the generic formulation, we should note that the first step of the protocol in Figure 8.8, namely publicly agreeing on a curve E and a point G on E, can be performed a-priori, which means at some time in the past, for example, by putting curve and point into a public standard.

The (random) numbers α and β are Alice’s and Bob’s secret keys, respectively, and should never be disclosed. They compute the same shared secret, because

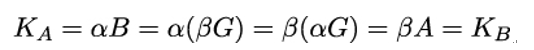
Diffie-Hellman key exchange example:

Take the elliptic curve

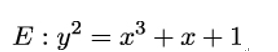
over 𝔽97 and the public point G = (76,82) on E. Alice’s secret key is the number α = 87. She computes the public point A = 87 ⋅G = (54,31) and sends it to Bob. Bob’s secret key is β = 13. He computes the public point B = 13 ⋅ G = (34,32) and sends it to Alice.

Both then proceed to compute the shared secret point K on E:

• Alice computes KA = 87 ⋅ (34,32) = (45,31)
• Bob computes KB = 13 ⋅ (54,31) = (45,31)

They can now use the x coordinate of K as their shared secret.

Double-and-add algorithm:

Going through the previous example, maybe you have wondered how, for example, Bob computes B = 13 ⋅G on E. One simple way would be just to add G to itself 13 times, but there is a better way to compute a product nP on E.

Just like in Chapter 7, Public-Key Cryptography, when we discussed the square-and-multiply algorithm for computing powers, we start by looking at the binary representation of the integer factor n:

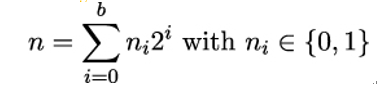
Now we have

The points 2i ⋅ P = 2 ⋅ (2i−1 ⋅ P) can be computed by repeated doubling of P. After that, the points 2i ⋅P, where ni = 1, are added. Therefore this algorithm is called double-and-add. In contrast to the naive repeated adding approach, which has a running time in 𝕆(n), the double-and-add algorithm has running time in 𝕆(log 2(n)), which is a massive improvement.

If an attacker, Eve, tries to break the key agreement based on elliptic curve Diffie-Hellman (ECDH) or some other cryptographic mechanism that uses an elliptic curve, she will learn the curve’s domain parameters, the base point G, and two points A,B on the curve, which are the product of G and some random, secret integers α and β, respectively.

Eve’s goal is to determine a secret integer α from the product αG she can observe. Whether she can do this efficiently – that is, in a polynomial time – or not, depends on the computational hardness of the ECDLP in the cyclic subgroup 𝔾 of E generated by the base point G.

While it is easy to solve ECDLP for cyclic groups with a small number of elements, it turns out that the best algorithms we know to solve it for large values require 𝒪() steps where n is the order of group 𝔾, that is, the number of elements in that group.

As a result, if Alice and Bob want their cryptographic algorithm to have a security level of, say, 128 bits, they can simply choose a secure curve where the order of group 𝔾 generated by a base point G is n ≥ 2256. This is because  = (2256) = 2128.

In the next section, we will discuss how secure curves can be chosen.