7.4.3 Authenticity of public keys

If Alice and Bob do not ensure that their public keys are authentic or do not verify their respective identities, they can suffer from a so-called man-in-the-middle attack, or MITM attack for short. In this attack, Mallory poses as Bob toward Alice and as Alice toward Bob, and provides her own public key to Alice and Bob. As a result, Alice and Bob will share a secret with Mallory, but not with each other. Figure 7.3 illustrates the attack.

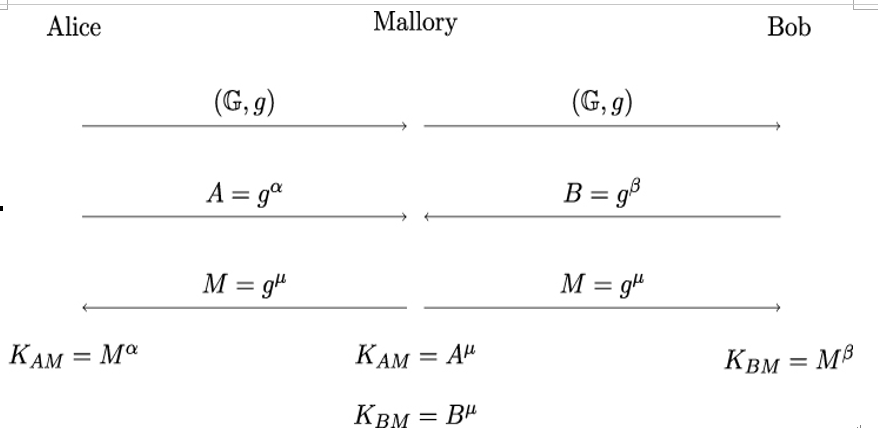
Figure 7.3: MITM attack on a Diffie-Hellman key exchange

One way to defend against this kind of attack is to use certificates (see Chapter 10, Digital Certificates and Certification Authorities) to obtain authentic copies of public keys and to enhance the pure key-exchange protocol with additional mechanisms that can provide entity authentication (see Section 7.9, Authenticated key exchange).

Another option that can also be relevant in the TLS context is using pre-shared (symmetric) keys to authenticate the public keys of Bob and Alice. Similarly, the public keys themselves can be shared out of band prior to the actual key exchange protocol.

7.5 The ElGamal encryption scheme

Without a doubt, you will have noticed that the Diffie-Hellman key exchange protocol is not yet a fully blown public-key scheme. While it accomplishes the task of sharing a secret over an insecure channel, which was the main motivation in thinking about public-key cryptosystems, it would still be nice to have actual encryption and decryption operations based on the discrete logarithm problem in the sense of Section 7.1.

Here, the ElGamal cryptosystem comes into play as an extension of the Diffie-Hellman key exchange protocol. The basic idea is very simple. Remember that in Diffie-Hellman key exchange, the triple PKAlice = (g,𝔾,A) can be seen as Alice’s public key. Assume Alice has published it on her web server. Bob wants to send Alice a message, so he retrieves (g,𝔾,A). The key observation is now that as soon as Bob chooses a private key SKBob = β, he already knows the shared secret KAB from the key exchange, so he might as well use it to encrypt his message m. Therefore, Bob sends the pair (B = gβ,c = eKAB(m)) to Alice, who can decrypt m by computing the shared secret KAB = Bα.

It only remains to specify the encryption function e. This relies on the observation that given a finite group 𝔾 with group operation ⋆ and an arbitrary element m ∈𝔾, multiplying m by a random element x ∈𝔾 gives another random element c ∈𝔾. Because the distribution of c is independent from that of m, c carries no information about m. Thus, to encrypt a message m ∈𝔾 for Alice, Bob simply computes c = m ⋆ x and sends c and his public key PKBob = B = gβ to Alice. To decrypt c, Alice first computes x = Bα and after that x−1 ∈𝔾. This can be done by the Extended Euclidean Algorithm (also see Section 7.7), which has a running time of O(log(x)) and recovers Bob’s original message via c ⋆ x−1 = m.

This encryption scheme even gives us perfect security if x is completely random, and Alice and Bob share it in advance. However, if we use a pseudo-random x instead of a random element, and define the pseudo-random x to be the shared secret from the Diffie-Hellman key exchange, the security of the algorithm is preserved because the pseudo-random x will look random for eavesdropper Eve.

Summing up, the ElGamal cryptosystem consists of the following steps:

• Plaintext Space and Ciphertext Space: The plaintext space ℳ and the ciphertext space 𝒞 are given by the elements of a cyclic group 𝔾.
• Key Pair Generation: Alice chooses a cyclic group (𝔾,⋆), a generator g, and an integer number α between 1 and the order of 𝔾. She computes A = gα and publishes PKAlice = (𝔾,g,A) as her public key, while she keeps SKAlice = α secret.
• Encryption: Bob retrieves PKAlice = (𝔾,g,A) and chooses some number β between 1 and the order of 𝔾 and a message m ∈ 𝔾. He computes B = gβ and x = Aβ. Then he encrypts m by multiplication: c = m ⋆ x. He then sends the pair (B,c) to Alice.
• Decryption: Alice computes x = Bα, using her private key. She then finds y = x−1 ∈𝔾 and retrieves m via c⋆y = (m⋆x)⋆x−1 = m⋆e = m.

Figure 7.4 illustrates the ElGamal cryptosystem. It is easy to see that the security of ElGamal relies on the same three assumptions as the Diffie-Hellman key exchange protocol, namely computational hardness of the discrete-logarithm and Diffie-Hellman problems and authenticity of the public key.

Figure 7.4: The ElGamal cryptosystem in a generic cyclic group 𝔾